Implementation¶
Organizational Chart¶
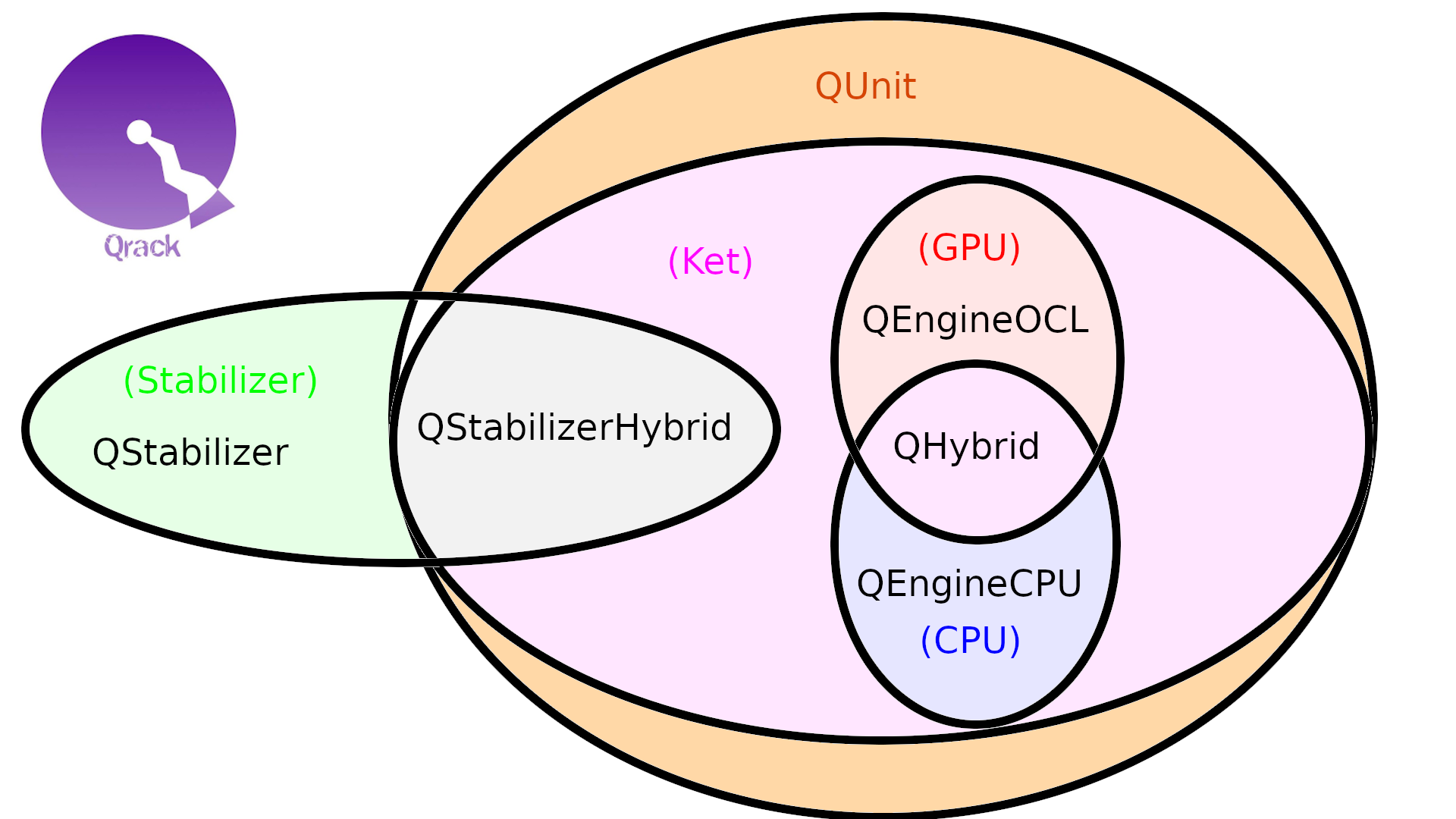
In overview, Qrack freely mixes simulator representations, between “Schrödinger method”/”ket,” stabilizer tableau, and Schmidt decomposed representations of both ket and stabilizer. Qrack::QStabilizerHybrid will attempt to maintain stabilizer representation for as deep as possible into a circuit, then switch over internally to ket representation when it encounters an operation it cannot carry out with Clifford and Pauli gates. For ket simulation, we have both CPU and GPU based implementations, which will be automatically switched between as opportune by QHybrid. QUnit creates a collection of partially Schmidt decomposed peer simulator types, like QStabilizerHybrid representation over QHybrid (or QPager, for Intel-QS-like “paged” simulation across different maximum allocation segments on one or more GPU devices).
QEngine¶
A Qrack::QEngine stores a set of permutation basis complex number coefficients and operates on them with bit gates and register-like methods.
The state vector indicates the probability and phase of all possible pure bit permutations, numbered from \(0\) to \(2^N-1\), by simple binary counting. All operations except measurement should be “unitary,” except measurement. They should be representable as a unitary matrix acting on the state vector. Measurement, and methods that involve measurement, should be the only operations that break unitarity. As a rule-of-thumb, this means an operation that doesn’t rely on measurement should be “reversible.” That is, if a unitary operation is applied to the state, their must be a unitary operation to map back from the output to the exact input. In practice, this means that most gate and register operations entail simply direct exchange of state vector coefficients in a one-to-one manner. (Sometimes, operations involve both a one-to-one exchange and a measurement, like the QInterface::SetBit method, or the logical comparison methods.)
A single bit gate essentially acts as a \(2\times2\) matrix between the \(0\) and \(1\) states of a single bits. This can be acted independently on all pairs of permutation basis state vector components where all bits are held fixed while \(0\) and \(1\) states are paired for the bit being acted on. This is “embarassingly parallel.”
To determine how state vector coefficients should be exchanged in register-wise operations, essentially, we form bitmasks that are applied to every underlying possible permutation state in the state vector, and act an appropriate bitwise transformation on them. The result of the bitwise transformation tells us which input permutation coefficients should be mapped to each output permutation coefficient. Acting a bitwise transformation on the input index in the state vector array, we return the array index for the output, and we move the double precision complex number at the input index to the output index. The transformation of the array indexes is basically the classical computational bit transformation implied by the operation. In general, this is again “embarrassingly parallel” over fixed bit values for bits that are not directly involved in the operation. To ease the process of exchanging coefficients, we allocate a new duplicate permutation state array vector, which we output values into and replace the original state vector with at the end.
The act of measurement draws a random double against the probability of a bit or string of bits being in the \(1\) state. To determine the probability of a bit being in the \(1\) state, sum the probabilities of all permutation states where the bit is equal to \(1\). The probablity of a state is equal to the complex norm of its coefficient in the state vector. When the bit is determined to be \(1\) by drawing a random number against the bit probability, all permutation coefficients for which the bit would be equal to \(0\) are set to zero. The original probabilities of all states in which the bit is \(1\) are added together, and every coefficient in the state vector is then divided by this total to “normalize” the probablity back to \(1\) (or \(100\%\)).
In the ideal, acting on the state vector with only unitary matrices would preserve the overall norm of the permutation state vector, such that it would always exactly equal \(1\), such that on. In practice, floating point error could “creep up” over many operations. To correct we this, Qrack can optionally normalize its state vector, depending on constructor arguments. Specifically, normalization is enabled in tandem with floating point error mitigation that floors very small probability amplitudes to exactly 0, below the estimated level of typical systematic float error for a gate like “H.” In fact, to save computational overhead, since most operations entail iterating over the entire permutation state vector once, we can calculate the norm on the fly on one operation, finish with the overall normalization constant in hand, and apply the normalization constant on the next operation, thereby avoiding having to loop twice in every operation.
Qrack has been implemented with float precision complex numbers by default. Optional use of double precision costs us basically one additional qubit, entailing twice as many potential bit permutations, on the same system. However, double precision complex numbers naturally align to the width of SIMD intrinsics. It is up to the developer, whether precision and alignment with SIMD or else one additional qubit on a system is more important.
QUnit¶
Qrack::QUnit is a “fundamentally” optimized layer on top of Qrack::QEngine types. QUnit optimizations include a broadly developed, practical realization of “Schmidt decomposition,” (see [Pednault2017],) per-qubit basis transformation with gate commutation, 2-qubit controlled gate buffering and “fusion,” optimizing out global phase effects that have no effect on physical “observables,” (i.e. the expectation values of Hermitian operators,) a classically efficient SWAP still equivalent to the quantum operation, and many “syngeristic” and incidental points of optimization on top of these general approaches. Publication of an academic report on Qrack and its performance is planned soon, but the Qrack::QUnit source code is freely publicly available to inspect.
VM6502Q Opcodes¶
This extension of the MOS 6502 instruction set honors all legal (as well as undocumented) opcodes of the original chip. See [6502ASM] for the classical opcodes.
The accumulator and X register are replaced with qubits. The Y register is left as a classical bit register. A new “quantum mode” and number of new opcodes have been implemented to facilitate quantum computation, documented in MOS-6502Q Opcodes.
The quantum mode flag takes the place of the unused flag bit in the original 6502 status flag register. When quantum mode is off, the virtual chip should function exactly like the original MOS-6502, so long as the new opcodes are not used. When the quantum mode flag is turned on, the operation of the other status flags changes. An operation that would reset the “zero,” “negative,” or “overflow” flags to 0 does nothing. An operation that would set these flags to 1 instead flips the phase of the quantum registers if the flags are already on. In quantum mode, these flags can all be manually set or reset with supplementary opcodes, to engage and disengage the conditional phase flip behavior. The “carry” flag functions in addition and subtraction as it does in the original 6502, though it can exist in a state of superposition. A “CoMPare” operation overloads the function of the carry flag in the original 6502. For a “CMP” instruction in the quantum 6502 extension, the carry flag analogously flips quantum phase when set, if the classical “CMP” instruction would usually set the carry flag. The intent of this flag behavior, setting and resetting them to enable conditional phase flips, is meant to enable quantum “amplitude amplification” algorithms based on the usual status flag capabilities of the original chip.
When an operation happens that would necessarily collapse all superposition in a register or a flag, the emulator keeps track of this, so it can know when its emulation is genuinely quantum as opposed to when it is simply an emulation of a quantum computer emulating a 6502. When quantum emulation is redundant overhead on classical emulation, the emulator is aware, and it performs only the necessary classical emulation. When an operation happens that could lead to superposition, the emulator switches back over to full quantum emulation, until another operation which is guaranteed to collapse a register’s state occurs.