Qrack Performance¶
Abstract¶
The Qrack quantum simulator is an open-source C++ high performance, general purpose simulation supporting arbitrary numbers of entangled qubits. While there are a variety of other quantum simulators such as [QSharp], [QHiPSTER], and others listed on [Quantiki], Qrack represents a unique offering suitable for applications across the field.
A selection of performance tests are identified for creating comparisons between various quantum simulators. These metrics are implemented and analyzed for Qrack. These experimentally derived results compare favorably against theoretical boundaries, and out-perform naive implementations for many scenarios.
Introduction¶
There are a growing number of quantum simulators available for research and industry use. Many of them perform quite well for smaller number of qubits, and are suitable for non-rigorous experimental explorations. Fewer projects are suitable for the growing mid-tier range of experimentation in the 20-30 qubit range.
Despite the availability of a selection of implementations, very little has been established when comparing the performance between different simulators. Broadly, the substantial bottlenecks around memory and IO utilization have largely preempted analysis into CPU efficiencies and algorithmic optimizations. There are some exceptions, such as IBM’s Breaking the 49-Qubit Barrier in the Simulation of Quantum Circuits [Pednault2017] paper.
Qrack provides high performance in the 20-30 qubit range, as well as an open-source implementation in C++ suitable for utilization in a wide variety of projects. As such, it is an ideal test-bed for establishing a set of benchmarks useful for comparing performance between various quantum simulators.
Future publications will compare the performance of Qrack against other publicly available simulators, as rigorous implementations can be implemented.
Reader Guidance¶
This document is largely targeted towards readers looking for a quantum simulator that desire to establish the expected bounds for various use-cases prior to implementation.
Disclaimers¶
- Your Mileage May Vary - Any performance metrics here are the result of experiments executed with selected compilation and execution parameters on a system with a degree of variability; execute the supplied benchmarks on the desired target system for accurate performance assessments.
- Benchmarking is Hard - While we’ve attempted to perform clean and accurate results, bugs and mistakes do occur. If flaws in process are identified, please let us know!
Method¶
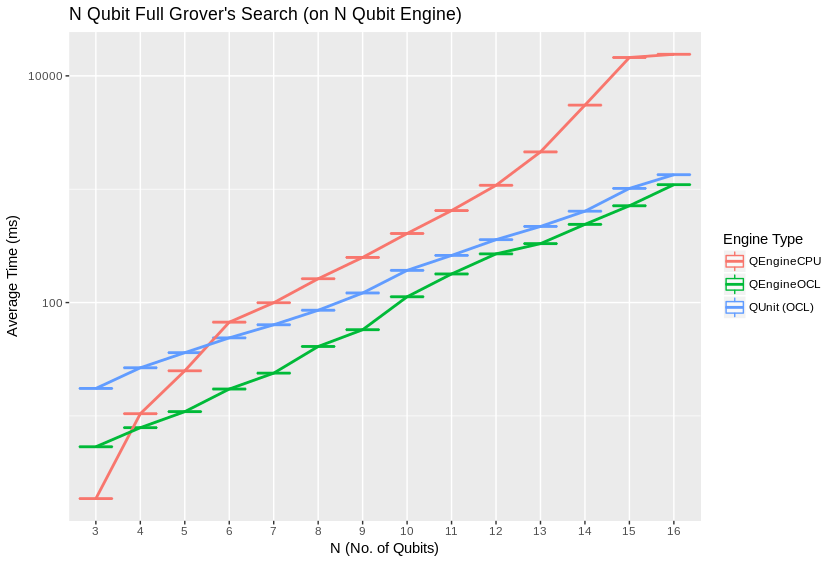
100 timed trials of each method were run for each qubit count between 3 and 28 qubits, on an AWS p3.8xlarge running Ubuntu Server 16.04LTS. The average and quartile boundary values of each set of 100 were recorded and graphed. Grover’s search to invert a black box subroutine, or “oracle,” was similarly implemented for trials between 3 and 16 qubits. Grover’s algorithm was iterated an optimal number of times, vs. qubit count, to maximize probability on a half cycle of the algorithm’s period, being \(floor\left[\frac{\pi}{4asin\left(1/\sqrt{2^N}\right)}\right]\) iterations for \(N\) qubits.
The 16 qubit data point for Grover’s search was not included for QEngineCPU, which is not hardware accelerated, because the monetary cost of exhaustive benchmarking is prohibitive, and QEngineCPU as currently implemented now primarily represents a legacy engine that would usually not be used for real application of Qrack. QEngineOCLMulti is experimental and generally performed worse or no better than QEngineOCL, despite running on multiple processors at once. It would also not yet be used for practical applications, so we omit its results, noting that it performs worse than the single device engine. (We will elaborate in the discussion section.)
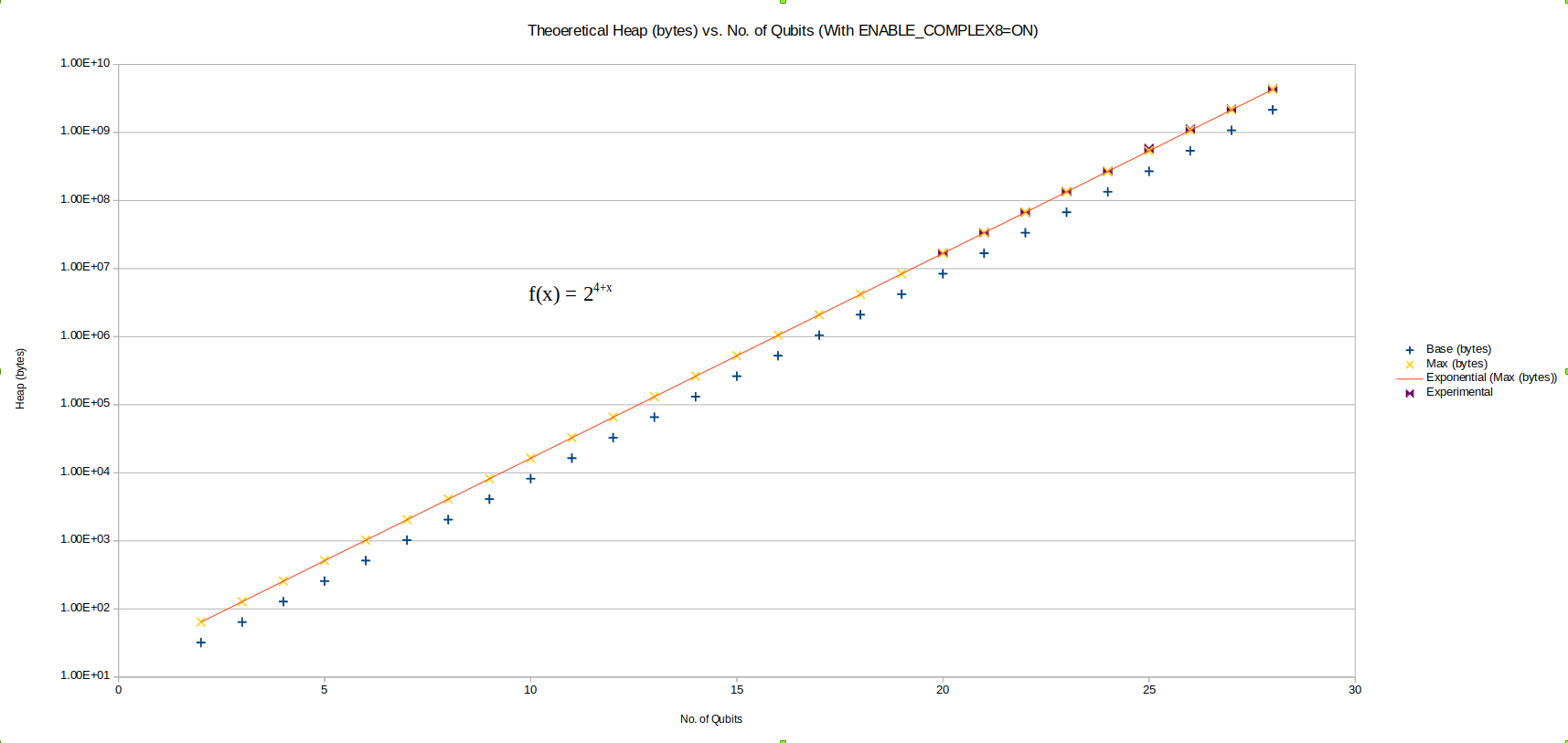
Heap profiling was carried out with Valgrind Massif. Heap sampling was limited but ultimately sufficient to show statistical confidence.
Results¶
We observed extremely close correspondence with theoretical complexity and RAM usage considerations for the behavior of all engine types. QEngineCPU and QEngineOCL require exponential time for a single gate on a coherent unit of N qubits. QUnit types with explicitly separated subsystems as per [Pednault2017] show constant time requirements for the same single gate.
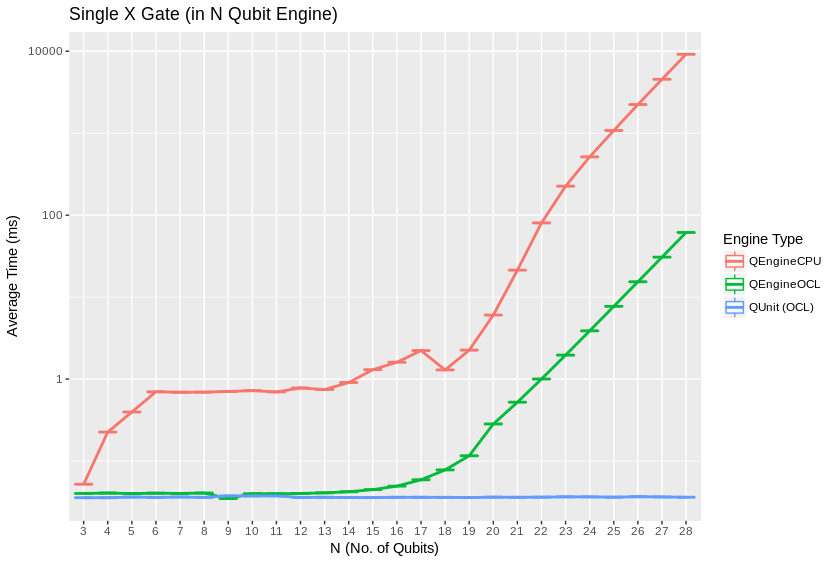
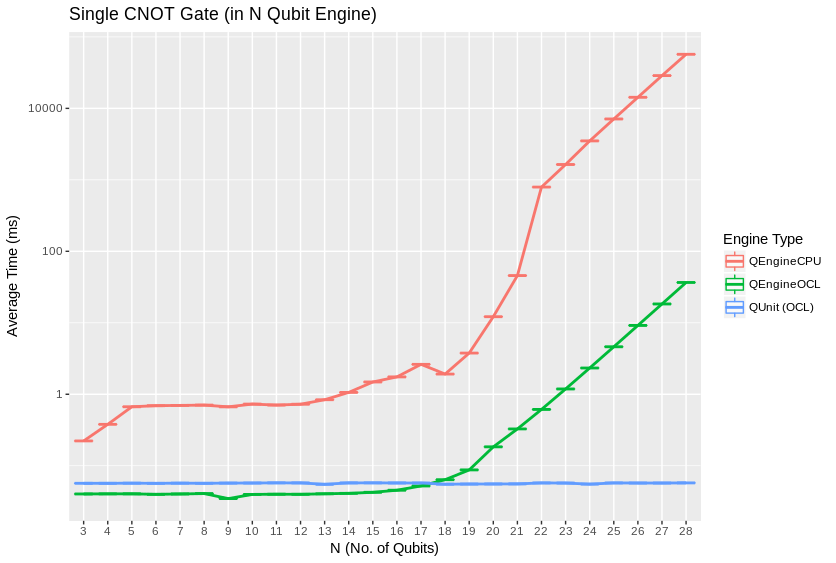
QEngineCPU and QEngineOCL can perform many identical gates in parallel across entangled subsystems for an approximately constant costs, when total qubits in the engine are held fixed as breadth of the parallel gate application is varied. To test this, we can apply parallel gates at once across the full width of a coherent array of qubits. (CNOT is a two bit gate, so \((N-1)/2\) gates are applied to odd numbers of qubits.) Notice in these next graphs how QEngineCPU and QEngineOCL have similar scaling cost as the single gate graphs above, while QUnit types show a linear trend (appearing logarithmic on an exponential axis scale):
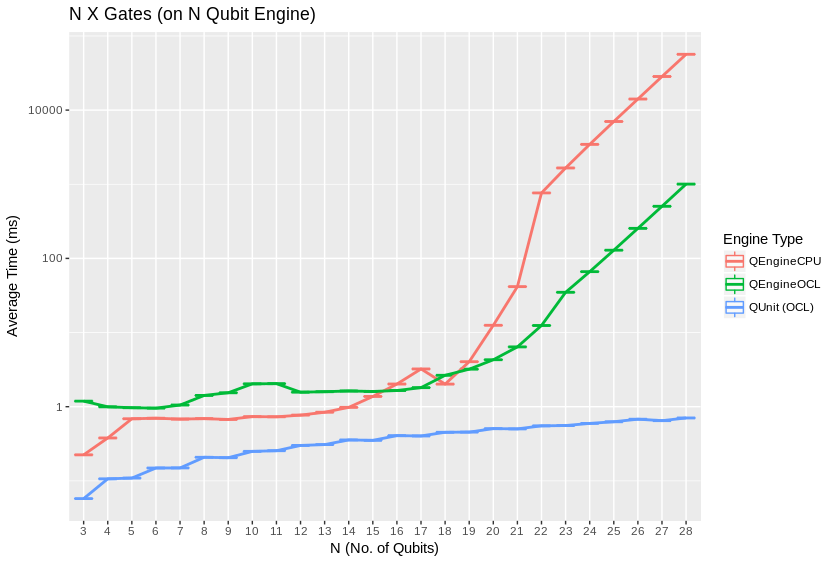
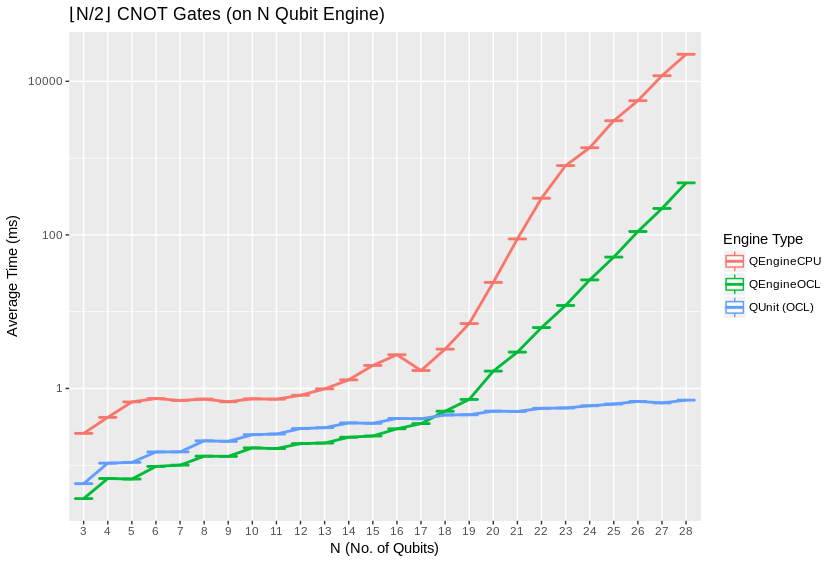
Heap sampling showed high confidence adherence to theoretical expecations. Complex numbers are represented as 2 double (64-bit) or 2 single (32-bit) accuracy floating point types, for real and imaginary components. The use of double or single precision is controlled by a compilation flag. There is one complex number per permutation in a separable subsystem of qubits. QUnit explicitly separates subsystems, while QEngine maintains complex amplitudes for all \(2^N\) permutations of \(N\) qubits. QEngines duplicate their state vectors once during most gates for speed and simplicity where it eases implementation.
Grover’s algorithm is a relatively ideal test case, in that it allows a modicum of abstraction in implementation while representing an ostensibly practical and common task for truly quantum computational hardware. For 1 expected correct function inversion result, there is a well-defined highest likelihood search iteration count on half a period of the algorithm for a given number of oracle input permutations to search. This graphs shows average time against qubit count for an optimal half period search:
[Broda2016] discusses how Grover’s might be adapted in practicality to actually “search an unstructured database,” or search an unstructured lookup table, and Qrack is also capable of applying Grover’s search to a lookup table with its IndexedLDA, IndexedADC, and IndexedSBC methods. Benchmarks are not given for this arguably more practical application of the algorithm, because few other quantum computer simulator libraries implement it, yet.
Discussion¶
Up to a consistent deviation at low qubit counts, speed and RAM usage is well predicted by theoretical complexity considerations of the gates, up to a factor of 2 on heap usage for duplication of the state vector.
We might speculate that, at high qubit counts, the calculations operate almost entirely on heap, while system call and cache hit efficiency consistently alter the trend up until a persistent and detectable “bump” at around roughly 8 qubits for the software implementation, and another “bump” at around 17 qubits for the hardware-accelerated engine, on the P3 test machine. For “software” simulation, this would be roughly consistent with a 4MB cache. For the hardware acceleration, this implies a preferred faster RAM bank of about 2GB.
QEngineOCLMulti, an OpenCL-based multiprocessor engine based on the algorithms developed in Intel’s [QHiPSTER], fails to outperform the single processor QEngineOCL. We include it in the current release to help the open source community realize a practical multiprocessor implementation in the context of Qrack. A branch of the multiprocessor engine has already been implemented with dynamic load balancing between processors, but it produced no significant improvement. By deduction, likely, we guess that the explicit reliance on general “host” RAM banks for storing the substate vectors creates a bottleneck, when multiple processors need to communicate with general RAM at the same time on the same bus. To alleviate this, a new QEngineOCLMulti implementation might assume that each processor device has a large personal store of memory, at least 4 or 8 GB, in which case OpenCL could be told explicitly to allocate substate vectors in device memory and not use “host” RAM at all for storing the state vector.
Further Work¶
Qrack has been successfully run on multiple processors at once, and even on clusters, but not with practical performance for real application; a good next step is to redesign the multiprocessor engine to actually outperform the single device engine. Also, CPU “software” implementation parallelism relies on certain potentially expensive standard library functionality, like lambda expressions, and might still be micro-optimized. The API offers many optimized bitwise parallel operations over contiguous bit strings, but similar methods for discontiguous bit sets should be feasible with bit masks, if there is a reasonable demand for them. Further, there is still opportunity for better constant bitwise parallelism cost coverage and better explicit qubit subsystem separation in QUnit.
We will also develop and maintain systematic comparisons to published benchmarks of quantum computer simulation standard libraries, as they arise.
Conclusion¶
Per [Pednault2017], explicitly separated subsystems of qubits in QUnit have a significant RAM and speed edge in many cases over the “Schrödinger algorithm” of QEngineCPU and QEngineOCL. One of Qrack’s greatest new optimizations to either general algorithm is constant complexity or “free” scaling of bitwise parallelism in entangled subsystems, compared to linear complexity scaling without this optimization. Qrack gives very efficient performance on a single node up to at least about 30 qubits, in the limit of maximal entanglement.
Citations¶
| [Broda2016] | Broda, Bogusław. “Quantum search of a real unstructured database.” The European Physical Journal Plus 131.2 (2016): 38. |
| [Pednault2017] | (1, 2, 3) Pednault, Edwin, et al. “Breaking the 49-qubit barrier in the simulation of quantum circuits.” arXiv preprint arXiv:1710.05867 (2017). |
| [QSharp] | Q# |
| [QHiPSTER] | QHipster |
| [Quantiki] | Quantiki: List of QC simulators |